Everything machines always wanted to learn about metal-oxide-semiconductor capacitors
by Tejas Govind Indani, Kunal Narayan Chaudhury, Sirsha Guha and Santanu Mahapatra , Tech Xplore
Machine learning (ML) is generally defined as data-driven technology mimicking intelligent human abilities, which bit by bit upgrades its accuracy from experience. It starts with gathering massive amounts of data, such as numbers, texts, images and so on. After training with the data, ML algorithms build a logical model to identify patterns through the least possible human intervention. With the help of sample training data, programmers test the model’s validity before introducing a new dataset. The more training data, the better the prediction.
However, we cannot expect reliable patterns or predictions on new data if the training dataset is biased, inconsistent or even wrong. But with the rapid expansion of this field, we can constrain ML models by enforcing a physics framework that consistently obeys natural laws.
In our recent work in Journal of Applied Physics, we have developed one such physically constrained ML model to gain insight into the electrostatics of a metal-oxide-semiconductor (MOS) capacitor, which is the fundamental building block of present CMOS (complementary metal-oxide-semiconductor) technology.
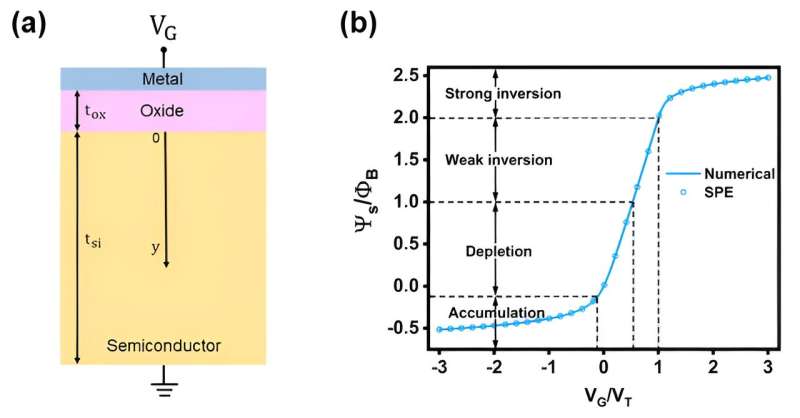
A MOS capacitor consists of a doped semiconductor body, a thin insulator (i.e., oxide) and a metal electrode called the gate. Depending upon the value of applied gate voltage, it operates in three modes: accumulation, depletion and inversion. In accumulation mode, mobile charge carriers similar to the dopant type form a thin layer by accumulating at the oxide-semiconductor interface.
With increasing gate voltage, the interface gradually becomes depleted of mobile charges, leaving immobile ions of the opposite polarity behind. It gives rise to an expanding potential drop at the semiconductor surface. With further escalation in gate voltage, a layer of mobile charge carriers of inverted dopant type but of similar concentration forms beneath the oxide-semiconductor interface. Hence, we say the MOS capacitor has entered into inversion mode.
The electrostatic of a MOS capacitor is governed by the Poisson-Boltzmann equation (PBE), which is a highly nonlinear differential equation (DE). A DE represents the interrelation between a function of one or more independent variables and its derivatives. The function signifies a physical quantity and the derivative indicates the rate of change with respect to the independent variables.
Solving nonlinear DEs on a computer is preferable since analytical solutions are usually tricky. Standard techniques (e.g., finite difference method, finite element method, shooting methods, splines) and user-friendly software packages built on these techniques are available for solving various DEs.
Neural networks (NNs), a subset of ML that has emerged in the recent past with significant impacts in several science and engineering disciplines, can solve nonlinear DEs effortlessly. They use interconnected nodes in a layered structure resembling the human brain, which makes biological neurons signal to one another.
NNs can accurately approximate complicated multivariate functions and deal with difficulties in conventional techniques, e.g., dependence on discretization in finite element methods and splines. The primary drawback of NNs is that their training is slow and computationally exhausting. However, we have prevailed over this challenge with improvements in computing and optimization techniques. Here, we investigate whether a machine can learn the physical principle of a MOS capacitor by solving the PBE using ML.
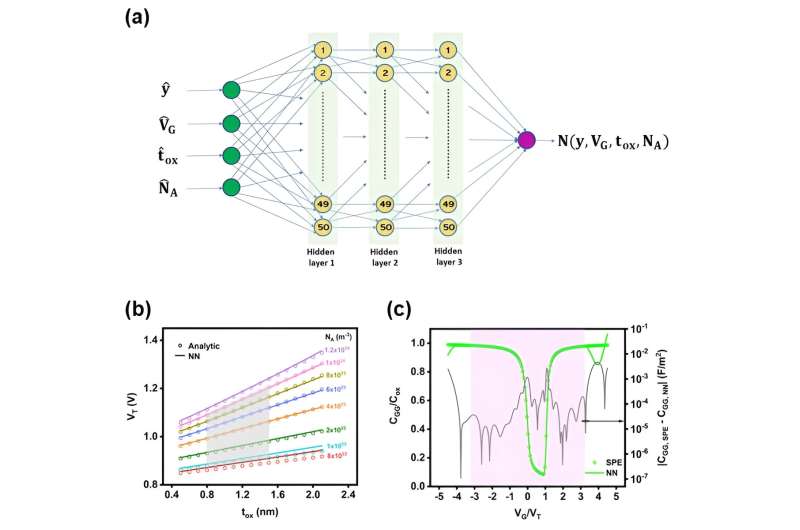
An approach called PINN (physics-informed neural network) has already become very popular for solving DEs arising from physical sciences (Burger equation, Schrodinger equation, etc.). Though it is pretty versatile and can be used to tackle any DE, the boundary conditions (BCs) are not hard-constrained in PINN.
Rather, along with the DE, they are combined as a penalty into a loss function, which computes the difference between predicted and actual values in the ML model. Therefore, it does not guarantee to satisfy the BCs exactly. On the other hand, Lagaris et al have proposed another technique to circumvent this issue.
It uses the governing equation to find a trial solution that properly fits the DE. This approach exactly satisfies the BCs. However, there is no general procedure to construct such trial solutions, especially for intricate boundary conditions we face in the case of an MOS capacitor.
Our approach to solving PBE for MOS capacitors is motivated by PINN and the method of Lagaris et al. Until now, the latter method has been employed to generate trials for Neumann and Dirichlet BCs, which is relatively straightforward. In comparison, our PBE requires both simple Dirichlet BC and complex Robin BC involving a function and its derivate.
Despite its highly nonlinear nature, we showed that it is challenging yet possible to use the method of Lagaris et al. to build trial solutions in a functional form (i.e., a function that takes one or more functions as arguments) that satisfies both BCs of the PBE. In our model, we have precisely sampled the physical domain of the device to construct the loss function from the trial solution.
The number of samples determines the complexity of computing the loss function and optimizing the trials. Therefore, we have conceived a physics-based sampling scheme and introduced device parameters stochastically into the model. This approach has assisted the model to attain exceptional accuracy.
We have validated our model against traditional numerical methods available in Python, as well as the industry-standard surface potential equation (SPE).
Through this study, we have found that our NN model can learn the relationship between input variables (i.e., thickness of the semiconductor, gate voltage, oxide thickness, and doping concentration) and the semiconductor potential.
Moreover, it is able to capture several relevant aspects of MOS device physics, such as the doping-dependent depletion width, variation of threshold voltage with oxide thickness and doping, and the low-frequency capacitance-voltage characteristics, in addition to interpreting the accumulation, depletion and inversion mechanisms. This model continues to obey device physics even outside the sampling domain.
In summary, for the first time, we report the possibility of an ML model to replicate the fundamental physics of MOS capacitors without using any labeled data (in contrast to typical supervised ML). We show that the commonly used PINN methodology fails to learn the Poisson-Boltzmann equation due to its dynamic nature posed by the unique boundary conditions.
We formulate a parametric model that naturally satisfies the boundary conditions so that the expressive power of neural networks can be harnessed to secure solutions with exceptional accuracy. In addition, we show that the proposed model can accurately capture critical insights such as depletion width, threshold voltage, inversion charge, etc.
This story is part of Science X Dialog, where researchers can report findings from their published research articles. Visit this page for information about ScienceX Dialog and how to participate.
More information:
Tejas Govind Indani et al, Physically constrained learning of MOS capacitor electrostatics, Journal of Applied Physics (2023). DOI: 10.1063/5.0168104
Tejas Indani is a former M.Tech. (AI) student of Indian Institute of Science (IISc) Bangalore. Kunal Narayan Chaudhury is working as Associate Professor at Indian Institute of Science (IISc) Bangalore. Sirsha Guha is a PhD student of Indian Institute of Science (IISc) Bangalore. Santanu Mahapatra is working as Professor at Indian Institute of Science (IISc) Bangalore. Homepage: sites.google.com/site/kunalnchaudhury/home
faculty.dese.iisc.ac.in/santanu/
Citation:
Everything machines always wanted to learn about metal-oxide-semiconductor capacitors (2023, November 22)
retrieved 23 November 2023
from https://techxplore.com/news/2023-11-machines-metal-oxide-semiconductor-capacitors.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no
part may be reproduced without the written permission. The content is provided for information purposes only.
Comments are closed